Hey there, welcome to Statssy! In this article, we will discuss the buzz and hype of Binomial Distribution. Let’s see if it gives you positive or negative vibes.
What’s the Hype About Binomial Distribution?
Hey there, cool cats and kittens! Ever heard of the binomial distribution and thought, “Ugh, sounds like a snooze fest?” Well, hold on to your TikTok, because we’re about to spill some tea that’ll make you go, “Whoa, that’s dope!”
So, What’s Binomial Distribution Anyway?
First off, let’s break it down. The binomial distribution is like the ultimate game of chance. Imagine you’re flipping a coin, rolling a dice, or even swiping right or left on Tinder. It’s all about predicting the outcome—will it be a heads or tails, a match or a pass? Binomial distribution helps you figure that out, but in a way that’s backed by some solid math.
Why Should You Even Care?
Okay, okay, I get it. You’re thinking, “Why does this even matter to me?” Well, you know how you love predicting the next viral trend or guessing who’s gonna win ‘Among Us’? Binomial distribution is like the secret sauce that can make your predictions way more accurate.
Applications You’ll Totally Vibe With
Now, let’s talk real-world stuff. This isn’t just for your math class; it’s everywhere! From figuring out how many people will actually show up to your Zoom party to predicting the next big hashtag on Twitter , binomial distribution has got you covered.
- Finance: Wanna invest in some crypto but are scared of the risks? The binomial distribution can help you play it smart.
- Social Media: Trying to become the next big influencer? Use binomial distribution to predict your follower growth.
- Gaming: Are you a ‘Fortnite’ fan? Calculate your win probabilities like a pro.
| What’s It All About? | Why Should You Care? | Real-World Vibes | Stats & Biostats Corner |
|---|---|---|---|
| Medicine: Will this new med give you side effects? | Wanna know if that new acne medicine will work without side effects? | Medicine: Predicting the number of patients experiencing side effects from new meds | 20% of patients reported side effects in clinical trials |
| Banking: Are these transactions legit? | Ever wondered how banks catch those sneaky fraudsters? | Banking: Estimating the number of fraudulent transactions | 5% increase in fraud cases last month |
| Email: How much spam will hit your inbox? | Tired of spam emails after online shopping? | Email: Predicting the number of spam emails you’ll get | Average person receives 10 spam emails per day |
| Gaming: Will you roll that lucky six? | Want to be the Yahtzee champ in your friend group? | Gaming: Chances of rolling a six in a dice game | 16.67% chance of rolling a six |
| Marketing: Will people click that ‘Buy Now’ button? | Want to know if your startup’s ad campaign will be a hit? | Marketing: Customer conversion rates | 30% conversion rate in last quarter’s ad campaign |
| Pharmaceuticals: Will this new drug actually work? | Curious about how effective new COVID vaccines are? | Pharmaceuticals: Efficacy of a new drug | 80% efficacy in recent drug trials |
| Politics: Who’s winning the next election? | Want to predict the next U.S. President? | Politics: Predicting vote counts for a candidate | 60% chance of winning based on current polls |
What Even is Binomial Distribution?
Definition and Core Concepts
Hey there, future probability wizards! Ever found yourself wondering what the odds are of something happening? Like, what are the chances of you acing that math test or your TikTok going viral? Well, that’s where Binomial Distribution comes into play!
In the simplest terms, Binomial Distribution is like your personal fortune teller for life’s yes-or-no questions. It’s all about predicting two possible outcomes: either something happens (that’s a win! ) or it doesn’t (bummer ).
Imagine you’re flipping a coin. It can either land heads up or tails up, right? Binomial Distribution helps you figure out the probability of getting a certain number of heads in a specific number of coin flips. So, if you’re flipping that coin 10 times, how many times will it land heads up? Binomial Distribution has got your back!
Properties of Binomial Distribution
Okay, so you’re probably thinking, “Cool, but what makes Binomial Distribution tick?” Great question! There are some key properties you gotta know:
- Fixed Number of Trials: You know exactly how many times you’re gonna try something, like flipping that coin 10 times.
- Two Possible Outcomes: It’s all about success (yay! ) or failure (aww ).
- Constant Probability: The chance of success stays the same each time, like a 50-50 shot in a coin flip.
- Independent Trials: What happens in one trial doesn’t affect the others. So, each coin flip is its own mini-adventure!
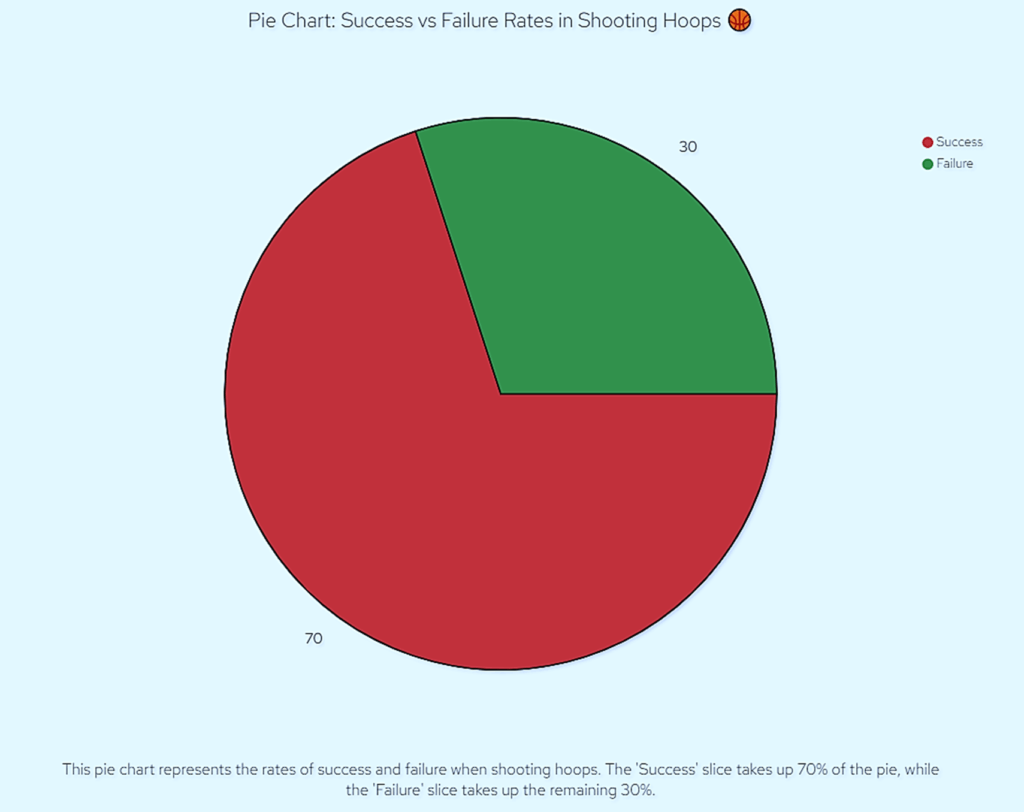
Chart: Pie Chart of Success vs Failure Rates
To make this even clearer, let’s visualize it! Picture a pie chart where one slice represents the rate of success and the other slice represents the rate of failure. If you’re flipping a fair coin, each slice would be 50% of the pie. But if you’re, say, shooting hoops and you make 70% of your shots, the ‘success’ slice would take up 70% of the pie, and the ‘failure’ slice would be the remaining 30%.
The Rules of the Game: Conditions for Binomial Distribution
Conditions and Successive Trials
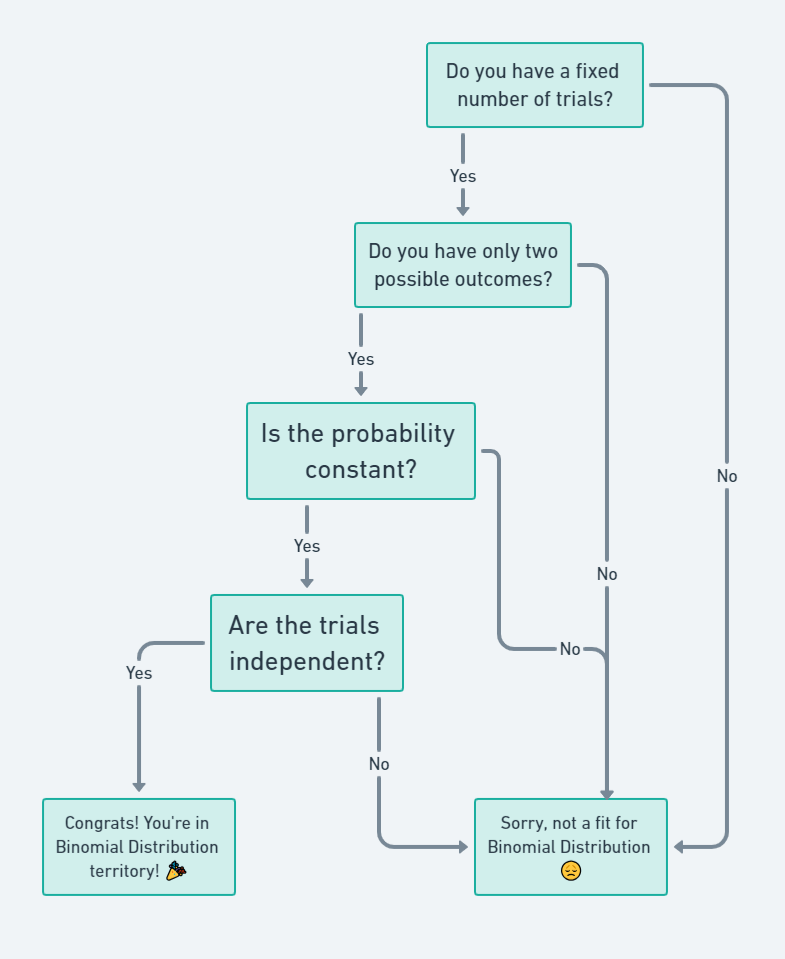
So, you’re vibing with the whole Binomial Distribution thing, huh? But wait, there’s a catch! Not every situation is a good fit for Binomial Distribution. There are some ground rules, or conditions, you gotta meet.
What are the conditions for binomial distribution?
- Fixed Number of Trials: You gotta know how many times you’re gonna try something. Like, if you’re flipping a coin, you need to decide in advance how many flips you’re gonna do.
- Two Possible Outcomes: It’s either a win or a loss, baby!
- Constant Probability: The odds gotta stay the same each time. So, if you have a 50% chance of winning a game, those odds can’t change mid-way.
- Independent Trials: What happens in Vegas, stays in Vegas! Each trial should not affect the other trials.
In binomial distribution, successive trials are…
Successive trials are like episodes of your favorite Netflix series —each one is its own thing but part of a bigger story. In Binomial Distribution, each trial is independent, meaning what happened in the last trial won’t spill over into the next one. So, if you failed the last time, don’t sweat it; you’ve got a clean slate each time!
Let me give you a flowchart that helps you figure out if your situation is right for Binomial Distribution
Bernoulli Trials: The OG of Binomial Distribution
What are Bernoulli Trials?
Alright, let’s spill the tea on Bernoulli Trials! Imagine you’re playing a super basic game on your phone. You tap the screen, and you either score a point or you don’t. That’s it. No power-ups, no extra lives, just a simple win or lose scenario.
This is what Bernoulli Trials are all about. They’re like the most basic level of a video game, where you have only two outcomes: success or failure. And guess what? These simple Bernoulli Trials are the building blocks of something way cooler—the Binomial Distribution!
So, in simpler terms, if Binomial Distribution was a blockbuster movie, Bernoulli Trials would be the trailer. It gives you a sneak peek into what the whole thing is about but in a much simpler format.
Real-World Connections
Okay, let’s bring this down to Earth with some examples you’ll totally relate to.
Instagram Polls
You know those Instagram polls where you have to choose between “Hot” or “Not”? Each time you vote, you’re actually participating in a Bernoulli Trial! The poll itself is like a mini-experiment with only two possible outcomes: either the majority agrees with you, or they don’t. And the best part? You get instant gratification by seeing the results in real-time!
TikTok Challenges
Ever tried to do one of those viral TikTok challenges? Whether it’s the “Renegade” dance or the “Bottle Cap Challenge,” each attempt you make is a Bernoulli Trial. You either nail it and get tons of likes and shares, or you mess up and become a meme. Either way, it’s a win-win, right?
The Secret Sauce: Binomial Distribution Formula
The Formula Unveiled
Okay, so you know when you’re cooking and you find that one secret ingredient that just makes the dish pop? Well, in the world of Binomial Distribution, the formula is that secret ingredient. It’s like the cheat code that helps you unlock all the levels in a video game.
So, what’s the formula? Don’t worry, we’re not going to throw a bunch of scary math symbols at you. Instead, think of it like a recipe. You’ve got your number of trials (let’s call it ‘n’), your probability of success (that’s ‘p’), and you’re trying to find out how many times you’ll actually succeed (that’s ‘x’).
Examples of Binomial Distribution
| Example | Scenario | How Binomial Distribution Fits In | Why It’s Cool |
|---|---|---|---|
| Among Us: Finding the Impostor | You’re playing Among Us and you’re trying to find out who the impostor is among 10 players. | Use the Binomial Distribution formula to calculate the odds of guessing the impostor correctly on your first, second, or third try. | It’s like having a cheat sheet to win the game! |
| Viral TikTok Dance Challenges: Renegade | You’re trying to nail the “Renegade” dance challenge in one go. | The formula can help you figure out the probability of nailing the dance in one, two, or three tries. | You can impress your friends by predicting your TikTok success! |
| Twitter Polls: Pineapple on Pizza? | A Twitter poll asks, “Is pineapple an acceptable pizza topping?” | Use the formula to predict the final outcome based on early voting trends. | You can be the Twitter oracle and predict poll outcomes! |
| Instagram Filters: Which One Will Go Viral? | You’re testing out new Instagram filters and wondering which one will get you the most likes. | Use the formula to calculate the odds of each filter making your post go viral. | Be the trendsetter and know which filter is the golden ticket! |
| Fortnite: Victory Royale | You’re in a Fortnite match and you want to be the last one standing. | Use Binomial Distribution to calculate your odds of winning based on your past performance. | Know your odds and strategize like a pro gamer! |
| Netflix Binge: To Continue or Not? | You’re watching a new series and can’t decide if you should binge-watch it. | Use the formula to determine the odds of the next episodes being as good as the first. | Make the ultimate binge-watch decision like a Netflix guru! |
What’s the Vibe? Characteristics of Binomial Distribution
Mean, Variance, and Standard Deviation
The Mean: The Average Outcome
The mean (μ) in a Binomial Distribution represents the average number of successes you can expect in a given number of trials. For example, if you toss a coin 10 times, the mean tells you that you can expect to get heads about 5 times. It’s calculated as μ = n × p, where n is the number of trials and p is the probability of success.
The Variance: How Spread Out Are the Outcomes?
The variance (σ²) measures the dispersion or how much the outcomes can vary from the mean. In real life, if you’re playing a game of darts, a low variance would mean most of your darts land close to the bullseye (the mean), while a high variance would mean the darts are spread out over the dartboard. The formula for variance in Binomial Distribution is σ² = n × p × (1-p).
Standard Deviation: The “Average” Difference
The standard deviation (σ) is essentially the “average” distance from the mean. It’s useful for understanding the range within which most outcomes will fall. For instance, in a class test, if the mean score is 70 and the standard deviation is 10, you can expect most students to score between 60 and 80. Standard Deviation is the square root of the variance: σ = √(n × p × (1-p)).
Examples, Interpretations, and Real-World Impact
| Example | Mean (μ) | Variance (σ²) | Standard Deviation (σ) | Real-World Interpretation | Real-World Impact |
|---|---|---|---|---|---|
| Tossing a coin 10 times, p = 0.5 | 5 | 2.5 | 1.58 | On average, you’ll get 5 heads. The outcomes will typically vary by about 1.58 heads from the mean. | If you’re betting on heads, you can expect to win about half the time, but don’t be surprised if you win 3 or 7 times out of 10. |
| Rolling a die 6 times, p = 1/6 | 1 | 0.83 | 0.91 | On average, you’ll roll one six. The outcomes will typically vary by about 0.91 from the mean. | In a board game, don’t count on rolling a six every time. You might get zero or even two sixes in 6 rolls. |
| 20 free throws in basketball, p = 0.75 | 15 | 3.75 | 1.94 | On average, you’ll make 15 shots. The outcomes will typically vary by about 1.94 shots from the mean. | If you’re a basketball player, you can expect to make around 15 shots, but a bad day could see you making only 13, and a good day could see you making 17. |
| 8 questions in a quiz, p = 0.6 | 4.8 | 1.92 | 1.39 | On average, you’ll get 4.8 questions right. The outcomes will typically vary by about 1.39 questions from the mean. | If you’re taking a quiz, you can expect to get around 5 questions right, but you might score as low as 3 or as high as 6 depending on the day. |
| 12 spins on a roulette wheel, p = 18/38 | 5.68 | 1.79 | 1.34 | On average, you’ll win 5.68 spins. The outcomes will typically vary by about 1.34 spins from the mean. | If you’re gambling, you can expect to win around 6 times, but luck could see you winning only 4 or as many as 7 spins. |





