93 / 100

Welcome to the world of data analytics! Today, we’re going to dive into the fascinating realm of descriptive statistics using Stata, a powerful statistical software. Whether you’re a student, a researcher, or a data enthusiast, this guide will help you understand and apply descriptive statistics in your projects.

What are Descriptive Statistics?

Descriptive statistics are a set of brief descriptive coefficients that summarize a given data set. They provide simple summaries about the sample and the measures. These summaries may be either a quantitative summary (mean, standard deviation, etc.) or a graphical summary (bar graph, histogram, etc.).

Why Use Stata for Descriptive Statistics?

Stata is a comprehensive statistical software that provides everything you need for data analysis and management. It’s user-friendly and has a wide range of commands for performing descriptive statistics.

Getting Started with Stata

Before we dive into the commands, let’s understand how to import data into Stata. You can import data from various file formats such as Excel, CSV, and more. Here’s a simple command to import a CSV file:

import delimited using "C:/path_to_your_file/your_file.csv"

Replace “path_to_your_file” and “your_file.csv” with the actual path and filename of your CSV file. For explanation purposes, I will be using a sample data here. Copy and paste it in Stata to generate dataset We’ll have three variables: influencer_name, followers, and posts.

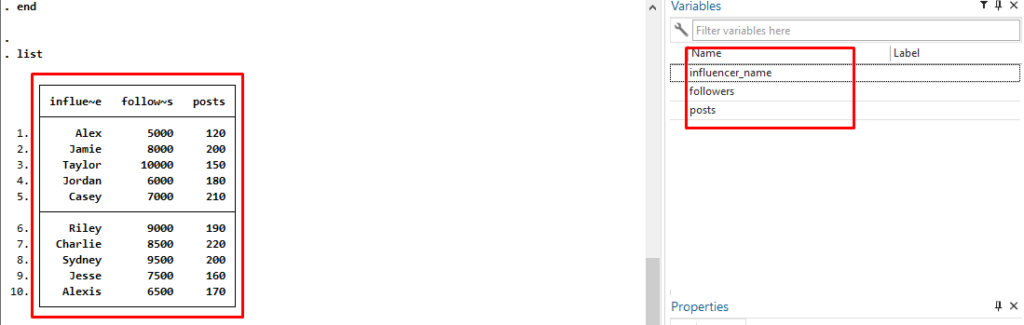
clear
input str20 influencer_name followers posts
"Alex" 5000 120
"Jamie" 8000 200
"Taylor" 10000 150
"Jordan" 6000 180
"Casey" 7000 210
"Riley" 9000 190
"Charlie" 8500 220
"Sydney" 9500 200
"Jesse" 7500 160
"Alexis" 6500 170
end
list

This will create a dataset with 10 Instagram influencers, along with their follower counts and the number of posts they’ve made. You can copy and paste this code into Stata to create the dataset.

After running the commend you will see your dataset being created like this. Here you can see the data on the left side and variable names on the right side.

Calculating Descriptive Statistics in Stata

Now that we have our data in Stata, let’s calculate some descriptive statistics. The primary command for this in Stata is summarize or sum for short. Here’s how you can use it:

summarize variable_name

Replace “variable_name” with the name of the variable you want to analyze. This command will give you the number of observations, mean, standard deviation, minimum, and maximum values for the specified variable.

For instance, let’s say we have a dataset of Instagram influencers and we want to calculate the average number of followers. Our command would look like this:

summarize followers

This will give us the descriptive statistics for the “followers” variable.

Mastering Descriptive Statistics in Stata: A Beginner’s Guide 2024

Interpreting the Results

Understanding the output is crucial. Let’s break down what each term means:

Observations: This is the total number of entries or data points for the variable.
Mean: This is the average value of the variable. It’s calculated by adding all the data points and dividing by the number of observations.
Standard Deviation: This measures the dispersion of a dataset relative to its mean. A low standard deviation means the data points tend to be close to the mean, while a high standard deviation indicates that the data points are spread out over a wider range.
Minimum and Maximum: These are the smallest and largest data points in your variable, respectively.

In our Instagram example, the mean would represent the average number of followers, the standard deviation would tell us how spread out the follower counts are, and the minimum and maximum would tell us the range of follower counts in our dataset.

The summarize command in Stata provides a statistical summary of the specified variable, in this case, followers. We can interpret them as:

Variable: This is the variable that you’re analyzing, which is followers in this case.
Obs: This is the number of observations, or data points, for the variable. In this case, there are 10 observations, meaning we have follower counts for 10 influencers.
Mean: This is the average value of the variable. It’s calculated by adding all the data points and dividing by the number of observations. In this case, the average number of followers across the 10 influencers is 7,700.
Std. Dev.: This is the standard deviation, which measures the dispersion of a dataset relative to its mean. A low standard deviation means the data points tend to be close to the mean, while a high standard deviation indicates that the data points are spread out over a wider range. In this case, the standard deviation is approximately 1,602.082, which suggests a moderate spread in the number of followers among the influencers.
Min and Max: These are the smallest and largest data points in your variable, respectively. In this case, the influencer with the fewest followers has 5,000 followers, and the influencer with the most followers has 10,000 followers.

So we can conclude that among the 10 Instagram influencers in our dataset, the average number of followers is 7,700. The number of followers varies, with a standard deviation of approximately 1,602. The influencer with the fewest followers has 5,000, while the influencer with the most followers has 10,000.

Descriptive Statistics for Multiple Variables

You can also calculate descriptive statistics for multiple variables at once by listing the variable names:

summarize variable1 variable2 variable3

So let’s take an example for that which also includes a special case,

summarize influencer_name posts

Running this command will give following result.

Mastering Descriptive Statistics in Stata:

Variable: These are the variables that you’re analyzing, which are influencer_name and posts in this case.
Obs: This is the number of observations, or data points, for each variable. In this case, there are 10 observations for the posts variable, meaning we have post counts for 10 influencers. For influencer_name, the number of observations is 0 because influencer_name is a string variable, and Stata doesn’t calculate descriptive statistics for string variables.
Mean: This is the average value of the variable. It’s calculated by adding all the data points and dividing by the number of observations. In this case, the average number of posts across the 10 influencers is 180.
Std. Dev.: This is the standard deviation, which measures the dispersion of a dataset relative to its mean. A low standard deviation means the data points tend to be close to the mean, while a high standard deviation indicates that the data points are spread out over a wider range. In this case, the standard deviation is approximately 30.55, which suggests a moderate spread in the number of posts among the influencers.
Min and Max: These are the smallest and largest data points in your variable, respectively. In this case, the influencer with the fewest posts has made 120 posts, and the influencer with the most posts has made 220 posts.

So we can conclude that among the 10 Instagram influencers in our dataset, the average number of posts is 180. The number of posts varies, with a standard deviation of approximately 30.55. The influencer with the fewest posts has made 120 posts, while the influencer with the most posts has made 220 posts.Mastering Descriptive Statistics

Conclusion

Descriptive statistics are a fundamental part of data analysis, and Stata provides a robust environment for calculating these statistics. Remember, the key to mastering Stata, like any other tool, is practice. So, keep exploring, keep learning, and keep analyzing!

Now for your quick reference I have created a basic diagram