Solving linear equations is a crucial skill in many fields including engineering and finance to data analysis and machine learning. R language, a very popular programming language for statistical computing, gives a simple and efficient way to solve linear equations using the solve() function. So lets learn the process of solving linear equations in R, step by step
Table of Contents
Step 1: Understand the Linear Equation System
A linear system can be represented in the form Ax = b, where A is a matrix of coefficients, x is a column vector of variables, and b is a column vector of constants. For example a linear system with two equations and two variables:
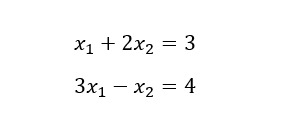
Can be written as
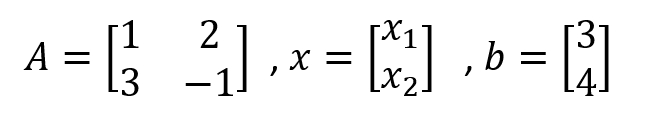
Where A is a 2X2 matrix since there are two equations and two variables. We will take more examples so don’t worry.
Now we can use matrix calculations on this to simplify and get values of x1 and x2.This can be done by hand or using R.
Need help with R?
Connect on Whatsapp
Step 2: So effectively what R does is it solves the linear system of equations using Matrix Algebra. So lets understand how to do it.
First you need to create matrices and vectors in R using the matrix () and c() functions, respectively. Here’s how to create A and b for the example above: Solving Linear Equations in R: A Complete Step-by-Step Guide with Examples using solve( ) Function Linear Equations in R
A <- matrix(c(1, 3, 2, -1), nrow = 2, ncol = 2, byrow = TRUE) b <- matrix(c(3, 4))
When you write & execute the above code in R, it will look something like this,

Step 3: Now we will use the solve() Function to Compute the Solution
The solve() function takes two arguments: the coefficient matrix A and the constant vector b.
solution <- solve(A, b)
The solve() function returns a vector containing the values of the variables that satisfy the linear system. For our example, the solution vector should look like this:
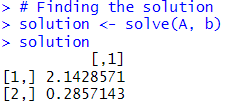
This means that the solution to the given linear system is x1 = 2.143 and x2 = 0.286
This means, mathematically we can write,
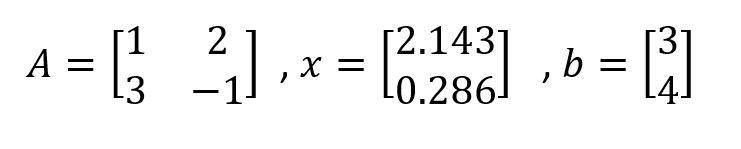
Step 4: Verify the Solution : Linear Equations in R
Finally to confirm if our solution is correct we can manual multiply A and solution matrix or in R, we can do this using the all.equal() function:
all.equal(A %*% solution, b)
If the result is TRUE, the solution is correct.
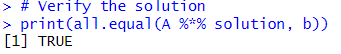
Conclusion
With this step-by-step guide, examples, and code snippets, you’re now well-equipped to tackle any linear equation problem using R.
R can be extremely helpful when solving long and complex system of linear equations. In the next article we will learn how to apply it to system of 3 or 4 equations.Linear Equations in R
Solving Linear Equations in R: A Complete Step-by-Step Guide with Examples using solve( ) Function





