Welcome to the world of probabilities, where every event has a chance of happening, and understanding these chances can open up a whole new perspective on the world around us. At Statssy, we’re all about making complex concepts like these accessible and engaging. Today, we’re diving into a fundamental concept in probability theory: how to find the probability of A or B.
Table of Contents
What is Probability?
Before we delve into the specifics, let’s take a moment to understand what probability is. In simple terms, probability is a measure of the likelihood that a particular event will occur. This measure is always a number between 0 and 1, where 0 indicates that the event will not occur, and 1 indicates that the event is certain to occur.
The Concept of Probability of A or B
When we talk about the probability of A or B, we’re referring to the chance that either event A occurs, event B occurs, or both events occur. This is a fundamental concept in probability theory and is used in a wide range of applications, from data analytics to machine learning.
There are three main scenarios to consider when finding the probability of A or B:
- Independent Events: These are events that do not affect each other. The occurrence of one does not change the probability of the occurrence of the other. For example, flipping a coin and rolling a die are independent events. The outcome of the coin flip does not affect the outcome of the die roll.
- Mutually Exclusive Events: These are events that cannot occur at the same time. If one event occurs, the other cannot. For example, getting a head or a tail on a single coin flip are mutually exclusive events.
- Dependent Events: These are events where the occurrence of one event does affect the probability of the occurrence of the other. For example, drawing cards from a deck without replacement is a dependent event because the outcome of the first draw affects the outcome of subsequent draws.
Now that we’ve covered the basics, let’s dive into how to find the probability of A or B in each of these scenarios.
Finding the Probability of A or B
Independent Events
When events A and B are independent, the probability of A or B is the sum of the probability of A and the probability of B. This can be represented by the formula:
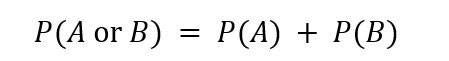
However, this formula assumes that A and B cannot occur at the same time. If they can, we need to subtract the probability of both A and B occurring from the total. This gives us the formula:
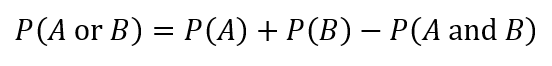
Mutually Exclusive Events
If events A and B are mutually exclusive (meaning they cannot both occur), then the probability of either A or B is simply the sum of their individual probabilities. This is because the occurrence of one event does not affect the occurrence of the other. The formula is the same as the first one for independent events:
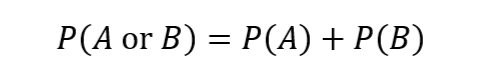
Dependent Events
When events A and B are dependent, finding the probability of A or B is a bit more complex. This is because the occurrence of one event changes the probability of the other event. In this case, we need to know not just the individual probabilities of A and B, but also the conditional probability of A given B (written as P(A|B)), or vice versa. The formula is:
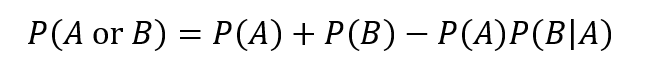
This formula tells us that the probability of A or B is the sum of the probabilities of A and B, minus the probability of A times the probability of B given A.
Now that we’ve covered the theory, let’s look at some examples to see how these formulas work in practice.
Examples of Finding the Probability of A or B
Let’s illustrate these concepts with some examples.
Independent Events
Suppose you’re flipping a coin and rolling a six-sided die. The event A is getting a head on the coin flip, and the event B is rolling a 6 on the die. These are independent events because the outcome of the coin flip doesn’t affect the outcome of the die roll.
The probability of getting a head on a coin flip (P(A)) is 0.5, and the probability of rolling a 6 on a die (P(B)) is 1/6. Using our formula for independent events:
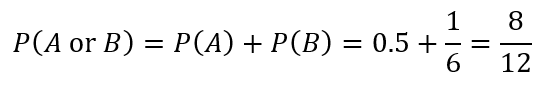
So, the probability of getting a head on the coin flip or rolling a 6 on the die is 7/12.
Mutually Exclusive Events
Consider a single card drawn from a standard deck of 52 cards. Let event A be drawing a king, and event B be drawing a queen. These are mutually exclusive events because a single card cannot be both a king and a queen.
The probability of drawing a king (P(A)) is 4/52 (as there are 4 kings in a deck), and the probability of drawing a queen (P(B)) is also 4/52. Using our formula for mutually exclusive events:
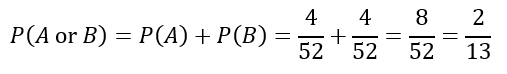
So, the probability of drawing either a king or a queen from a deck of cards is 2/13.
Dependent Events
Suppose you’re drawing two cards from a deck without replacement. The event A is drawing a king on the first draw, and the event B is drawing a queen on the second draw. These are dependent events because the outcome of the first draw affects the outcome of the second draw.
The probability of drawing a king on the first draw (P(A)) is 4/52. After drawing a king, there are only 51 cards left in the deck, so the probability of drawing a queen on the second draw (P(B|A)) is 4/51. Using our formula for dependent events:
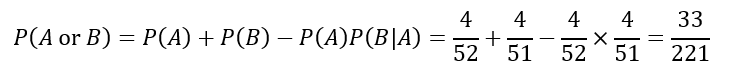
So, the probability of drawing a king on the first draw or a queen on the second draw is 17/221.
Understanding how to find the probability of A or B is a fundamental skill in data analytics and machine learning. If you’re interested in learning more about these topics, check out our data science courses at Statssy. We make complex concepts accessible and engaging, so you can gain the skills you need to excel in the data-driven world.
Now that you are clear with the concept, let us give you an overview of some real world cases where this concept is used in data analytics.
1. Medical Diagnosis: In healthcare analytics, the concept of probability is crucial. For instance, consider a patient showing symptoms like fever and cough. The doctor might want to know the probability of the patient having disease A (like the flu) or disease B (like COVID-19). By using the patient’s symptoms, medical history, and relevant data from similar cases, a data analytics model can help estimate these probabilities and assist in diagnosis.
2. Customer Segmentation: In marketing analytics, businesses often segment their customers into different groups based on purchasing behavior, demographic information, and other factors. For example, a retail company might want to know the probability of a customer falling into segment A (frequent, high-spending customers) or segment B (infrequent, low-spending customers). This information can then be used to tailor marketing strategies for each segment.
3. Risk Assessment: In finance, risk assessment is a key application of probability. For example, a bank might want to know the probability of a borrower defaulting on a loan (event A) or making a late payment (event B). By analyzing the borrower’s credit history, income level, and other relevant factors, a data analytics model can estimate these probabilities, helping the bank make informed lending decisions.
4. Weather Forecasting: Meteorologists use probability to make weather forecasts. For example, they might want to know the probability of it raining (event A) or snowing (event B) tomorrow. By analyzing weather patterns, atmospheric data, and other factors, a data analytics model can estimate these probabilities, leading to more accurate weather forecasts.
5. E-commerce Recommendations: E-commerce platforms often use probability to generate personalized product recommendations. For instance, based on a customer’s browsing history and purchase history, the platform might want to know the probability of the customer liking product A (a novel) or product B (a cookbook). A data analytics model can estimate these probabilities, helping the platform recommend products the customer is likely to enjoy.
6. Social Media Analysis: Social media platforms often analyze user behavior to tailor content. For example, based on a user’s past likes and shares, the platform might want to know the probability of the user liking post A (a news article) or post B (a funny video). A data analytics model can estimate these probabilities, allowing the platform to show content the user is likely to find interesting.
7. Sports Analytics: In sports analytics, teams often use probability to predict game outcomes. For example, based on past performance, a team might want to know the probability of them winning (event A) or the opposing team winning (event B) the next game. A data analytics model can estimate these probabilities, helping the team strategize effectively.
8. Quality Control: In manufacturing, probability is often used in quality control. For instance, a manufacturer might want to know the probability of a product being defective (event A) or not defective (event B). By analyzing production data, a data analytics model can estimate these probabilities, helping the manufacturer maintain high quality standards.
9. Traffic Management: In urban planning, probability is used to manage traffic. For example, based on traffic patterns, a city might want to know the probability of a traffic jam occurring at location A (a busy intersection) or location B (a less busy intersection). A data analytics model can estimate these probabilities, helping the city manage traffic flow and plan infrastructure.
10. Cybersecurity: In cybersecurity, probability is used to assess system vulnerabilities. For example, a company might want to know the probability of their system experiencing a security breach (event A) or remaining secure (event B). By analyzing system data and known vulnerabilities, a data analytics model can estimate these probabilities, helping the company plan their security measures more effectively.
Now that you have learnt the concept, let us quickly revise everything through some questions.
1. What is the probability of A or B?
The probability of A or B depends on whether the events are independent, mutually exclusive, or dependent. For independent events, it’s the sum of the probabilities of A and B, minus the probability of both A and B occurring. For mutually exclusive events, it’s simply the sum of the probabilities of A and B. For dependent events, it’s the sum of the probabilities of A and B, minus the probability of A times the probability of B given A.
2. What are independent events?
Independent events are events that do not affect each other. The occurrence of one does not change the probability of the occurrence of the other. For example, flipping a coin and rolling a die are independent events.
3. What are mutually exclusive events?
Mutually exclusive events are events that cannot occur at the same time. If one event occurs, the other cannot. For example, getting a head or a tail on a single coin flip are mutually exclusive events.
4. What are dependent events?
Dependent events are events where the occurrence of one event does affect the probability of the occurrence of the other. For example, drawing cards from a deck without replacement is a dependent event because the outcome of the first draw affects the outcome of subsequent draws.
5. How do I calculate the probability of A or B for independent events?
For independent events, the probability of A or B is given by the formula P(A or B) = P(A) + P(B) – P(A and B).
6. How do I calculate the probability of A or B for mutually exclusive events?
For mutually exclusive events, the probability of A or B is given by the formula P(A or B) = P(A) + P(B).
7. How do I calculate the probability of A or B for dependent events?
For dependent events, the probability of A or B is given by the formula P(A or B) = P(A) + P(B) – P(A)P(B|A).
8. Can you give an example of finding the probability of A or B?
Sure, let’s consider flipping a coin (event A) and rolling a six on a die (event B). These are independent events. The probability of getting a head on a coin flip is 0.5, and the probability of rolling a 6 on a die is 1/6. So, the probability of getting a head on the coin flip or rolling a 6 on the die is 0.5 + 1/6 = 7/12.
9. What is the importance of understanding the probability of A or B in data analytics and machine learning?
Understanding the probability of A or B is fundamental to making predictions and decisions based on data. It’s used in a wide range of applications, from predicting customer behavior to training machine learning models.
10. Where can I learn more about probability and other data analytics concepts?
You can learn more about these topics by taking our data science courses at Statssy. We make complex concepts accessible and engaging, so you can gain the skills you need to excel in the data-driven world.





