Empirical Rule Calculator in Statistics 2024
What is the empirical rule in statistics?
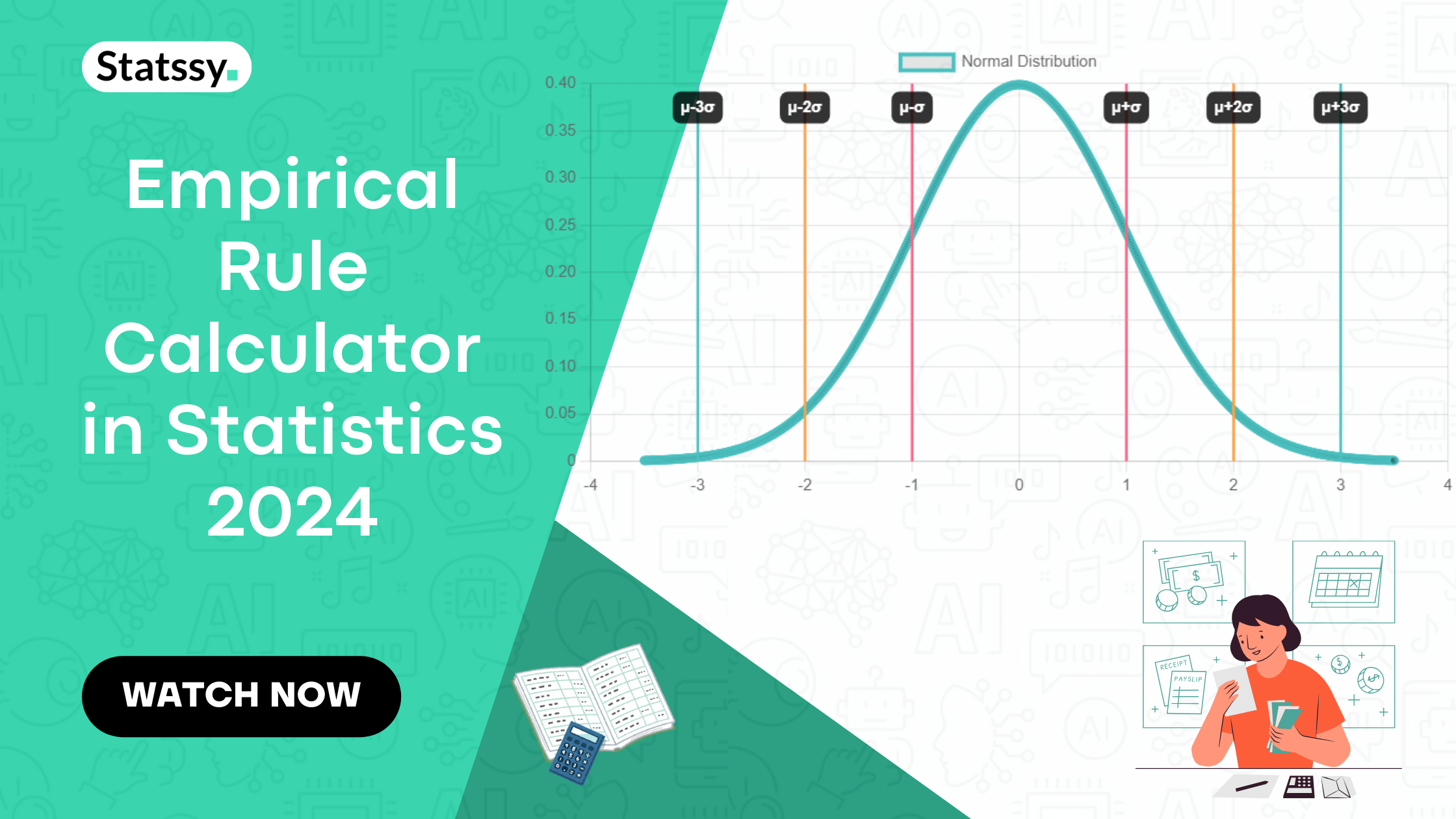
The empirical rule is also known as the 68-95-99.7 rule and it is a statistical rule which states that for a normal distribution:
- Approximately 68% of all data falls within one standard deviation of the mean.
- Approximately 95% of all data falls within two standard deviations of the mean.
- Approximately 99.7% of all data falls within three standard deviations of the mean.
This rule provides a quick estimate of the probability of data observed in a normal distribution which falls within a certain range, based on the mean and standard deviation.
For example, if you have a normal distribution with a mean (average) of 50 and a standard deviation of 10, then:
- 68% of the data will fall between 40 and 60 (mean ± 1 standard deviation).
- 95% of the data will fall between 30 and 70 (mean ± 2 standard deviations).
- 99.7% of the data will fall between 20 and 80 (mean ± 3 standard deviations).
Mathematically we can write,
- 68% of the data will lie between (μ-σ,μ+σ)
- 95% of the data will lie between (μ-2σ,μ+2σ)
- 99.7% of the data will lie between (μ-3σ,μ+3σ)
Use the Calculator Below to find empirical values
Empirical Rule Calculator
Real life use case of empirical rule :Empirical Rule Calculator
The empirical rule is a very practical rule used in the real life. Following are some of its use cases
- Standardized Test Scores - You must be aware of SAT or ACT! They are standardized tests designed to follow a normal distribution by there very nature. Let's say the average score on an SAT is 1000 with a standard deviation of 200. According to the empirical rule, about 68% of students should score between 800 and 1200, 95% should score between 600 and 1400, and almost all students (99.7%) should score between 400 and 1600.
- Human Height - The heights of adult males in many countries are approximately normally distributed. Let's assume the average height of an adult male in the U.S. is about 70 inches (about 5'10") with a standard deviation of about 3 inches. The empirical rule would suggest that 68% of men are between 67 and 73 inches tall, 95% are between 64 and 76 inches tall, and 99.7% are between 61 and 79 inches tall.
- Manufacturing and Quality Control - Suppose a factory produces screws with an average length of 5 cm and a standard deviation of 0.1 cm, and let the lengths are normally distributed. The empirical rule can help predict the proportion of screws within certain length ranges. It would suggest that 68% of screws are between 4.9 and 5.1 cm long, 95% are between 4.8 and 5.2 cm long, and 99.7% are between 4.7 and 5.3 cm long. Now this analysis helps in quality control and assurance processes.
- Temperature - If the average temperature in a city during the summer is 80 degrees Fahrenheit with a standard deviation of 5 degrees, and if the temperatures follow a normal distribution, the empirical rule suggests that about 68% of summer days will have a temperature between 75 and 85 degrees, about 95% of days will have a temperature between 70 and 90 degrees, and about 99.7% of days will have a temperature between 65 and 95 degrees.
Why Empirical Rule is important for data analysts?
- It help to understand data distribution - Understanding the distribution of data you are working on can help you easily (not very easily) identify hidden patterns in the data.
- Quick Estimations - The rule provides a fast way to estimate where most of the values in a data set lie, provided the data follows a normal distribution. This can be helpful in quickly understanding the data set and making predictions. For example if you know that your classmates' height is normally distributed, you can easily classify them in buckets of short heighted, medium heighted or tall.
- Outlier Detection - Outliers are points which do not behave the way it is expected to behave. Imagine a student in your class who is 85 years old! Probably you would not expect that person to be in class. Right? Its because the person is an outlier as most of your classmates are young people. Now statistically we say, if data is normally distributed, a value more than three standard deviations away from the mean is a potential outlier, as under the empirical rule, 99.7% of data should be within three standard deviations of the mean.
- Assumption Checking - Many statistical techniques like linear regression, ANOVA assume that data is normally distributed. Now using the empirical rule, you can easily determine what amount of your data falls in a given range. We will discuss this in detail later in other blogs.
- Communication - As a data analyst, you'll often need to explain your findings to non-technical stakeholders like your manager who probably don't give a shit about statistics. Now using empirical rule, you can make your explanations simple and easily digestible for your manager.
Why Empirical Rule is important for data scientists?
Now let me be very clear! To become a data scientist, you have to first be the data analyst. This means all points that I mentioned previously are important for data scientists as well. But few more which can help data scientists because data scientists do far more operations on data than data analyst.
- Model Assumptions - Many machine learning and statistical models like linear regression, logistic regression, Gaussian Naive Bayes make certain assumptions about the distribution of the data or the model's errors. Empirical rule can help assess whether these assumptions are reasonable.
- Exploratory Data Analysis (EDA) -The empirical rule is a useful tool during EDA because it will help to quickly summarize the data and identify potential outliers or unusual observations. Remember! here we not only analyze the outliers but something more than that. We will discuss this in detail in a different article.
- Feature Engineering - It is process of creating new input features for machine learning models. For instance, if a feature is not normally distributed, a data scientist might decide to transform it by taking the logarithm or doing some other operation to achieve a more normal distribution.
- Statistical Testing - The empirical rule can aid in hypothesis testing and the interpretation of p-values. It provides an intuitive understanding of standard deviations, which are fundamental to concepts like the standard error, confidence intervals, and z-scores.
- Predictive Modeling - When building predictive models it is important to understand the distribution of the target variable (Y) and the predictor variables (X) is crucial. The empirical rule provides a foundation for understanding these distributions and the relationships between them.
Now I hope you understood the concept of empirical rule. Happy Learning!!!!
Empirical Rule Calculator in Statistics 2024





