Data Transformation and Scaling in Stata for Beginners – Which one to choose and why?

Introduction
Hey there, social media enthusiasts and data wizards! Welcome to Statssy! Ever found yourself puzzled by the different ways people rate things? Maybe you’ve seen a 5-star rating for a YouTube video and a 10-point scale for a TikTok dance challenge. How do you compare these different scales? Welcome to the world of scale transformation!
Scale transformation is like the secret sauce that makes your social media data appetizing and meaningful. It’s all about changing the variable values to ensure they play nicely together, especially when you’re dealing with different scales like those pesky Likert scales in your social media surveys.
Imagine you’re conducting a survey to find out how much people love or hate the latest viral meme. Some folks might rate it on a scale of 1 to 5, while others might go all out with a 1 to 10 scale. How do you make sense of this mishmash? That’s where scale transformation comes into play, and trust me, it’s a game-changer in data analytics!
1. Z-Standardization
Ready to dive deeper? Let’s talk about Z-Standardization, one of the coolest kids on the scale transformation block.
Z-Standardization is like giving your data a uniform to wear. It’s all about rescaling your data to have a mean of 0 and a variance of 1. In simple terms, it’s about making different scales speak the same language.
Z Standardization Formula:
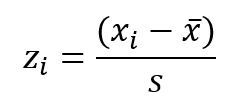
where xi is the individual observation, xbar is the mean of the observations, and s is the standard deviation.
Advantages:
- Consistency Across Different Scales: Whether you’re comparing likes, comments, or shares, Z-Standardization makes sure everything is on the same page. It’s like turning apples and oranges into fruit salad!
- Example: Imagine you’re analyzing the performance of your favorite influencer across different platforms. With Z-Standardization, you can compare engagement metrics like likes, comments, and shares seamlessly.
Disadvantages:
- Potential Loss of Original Scale Information: While it’s great for comparison, Z-Standardization might make you lose some nuances of the original scale. It’s like translating a joke from one language to another; sometimes, something gets lost in translation.
Social Media Example: Think about analyzing an influencer’s performance on Instagram. You want to see how their posts are doing in terms of likes, comments, and shares. Z-Standardization helps you put all these metrics on a level playing field, so you can see what’s really popping! Data Transformation and Scaling
So, next time you’re scratching your head over different rating scales on social media, remember Z-Standardization is your friend. Stay tuned for more insights on scale transformation, and happy analyzing!
Need help with R/Stata?
Connect on Whatsapp
2. Range Standardization
Hold on to your hashtags, because we’re about to explore another superstar of scale transformation: Range Standardization!
Range Standardization is like the DJ at a social media party, adjusting the beats to keep everyone dancing in sync. It’s all about scaling your data to a specific range, such as 0 to 1. How does it work? Let’s break it down:
Range Standardization Formula:
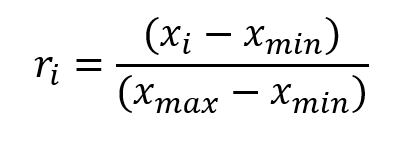
where xi is the individual observation, xmin is the minimum value of the observations, and xmax is the maximum value of the observations.
Advantages:
- Specific Range Scaling: Range Standardization lets you set the dance floor, defining the exact range you want your data to groove in. It’s super useful for cluster analysis, where you want to group similar things together.
- Example: Picture yourself analyzing trends across different social media platforms like Facebook, Twitter, and LinkedIn. Range Standardization helps you see the big picture, making sure all the trends are dancing to the same beat.
Disadvantages:
- Sensitivity to Outliers: Watch out for those party crashers! Range Standardization can be sensitive to outliers, those extreme values that can throw off the whole vibe. If one value is way off the charts, it can skew the whole transformation.
Social Media Example: Let’s say you’re comparing audience engagement on Instagram vs. TikTok. Maybe you want to see how a viral dance challenge is performing on both platforms. Range Standardization helps you put those engagement metrics on the same scale, so you can see which platform is really rocking the dance floor!
Range Standardization is like the perfect filter for your data analytics, helping you see the trends and patterns that matter most. So next time you’re diving into the data, remember to invite Range Standardization to the party. It’s sure to make your analysis pop!
Absolutely! Let’s dive into the practical application of scale transformations in Stata and gather some insights from industry experts.
Certainly! Let’s revise Part 4 with a more detailed step-by-step guide, including both Z-Standardization and Range Standardization for 20 records of fake data.
4. Practical Application of Scale Transformation in Stata
Consider a social media influencer who has posted the same 10 videos on both Instagram and TikTok. Now we have the ratings from Instagram out of 10 and from TikTok out of 5. So how should we compare which video performed better on which platform?
Here’s our dummy data:
Video_Number TikTok_Rating Instagram_Rating 1 5 10 2 3 7 3 4 8 4 2 5 5 4 9 6 3 6 7 5 8 8 2 4 9 3 7 10 4 9
Step 1: Create and Load Your Data in Stata You can manually enter this data into Stata using the following commands:
clear input Video_Number TikTok_Rating Instagram_Rating 1 5 10 2 3 7 3 4 8 4 2 5 5 4 9 6 3 6 7 5 8 8 2 4 9 3 7 10 4 9 end
Step 2: Z-Standardization To perform Z-Standardization, you can use the following commands:
egen TikTok_Mean = mean(TikTok_Rating) egen TikTok_SD = sd(TikTok_Rating) gen TikTok_Z = (TikTok_Rating - TikTok_Mean) / TikTok_SD egen Instagram_Mean = mean(Instagram_Rating) egen Instagram_SD = sd(Instagram_Rating) gen Instagram_Z = (Instagram_Rating - Instagram_Mean) / Instagram_SD
This will create new variables with the Z-scores for both TikTok and Instagram ratings. You can now compare these standardized scores across different scales. When you check the data tab you will find the two columns with Z-scores for TikTok and Instagram like this Data Transformation and Scaling
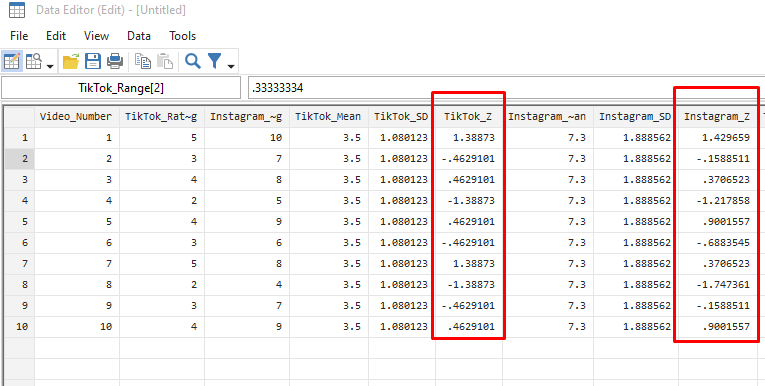
| Video_Number | Instagram_Z | TikTok_Z |
|---|---|---|
| 1 | 1.429659 | 1.38873 |
| 2 | -0.1588511 | -0.4629101 |
| 3 | 0.3706523 | 0.4629101 |
| 4 | -1.217858 | -1.38873 |
| 5 | 0.9001557 | 0.4629101 |
| 6 | -0.6883545 | -0.4629101 |
| 7 | 0.3706523 | 1.38873 |
| 8 | -1.747361 | -1.38873 |
| 9 | -0.1588511 | -0.4629101 |
| 10 | 0.9001557 | 0.4629101 |
Interpretation: Data Transformation
- Positive Z-Scores: Videos with positive Z-scores on both platforms performed above average. For example, the first video has positive Z-scores on both Instagram and TikTok, indicating that it performed well on both platforms.
- Negative Z-Scores: Videos with negative Z-scores performed below average. For example, the fourth video has negative Z-scores on both platforms, indicating that it performed poorly on both platforms.
- Comparing Platforms: By comparing the Z-scores, you can identify which videos performed relatively better on one platform over the other. For example, the fifth video has a higher Z-score on Instagram than on TikTok, indicating that it performed relatively better on Instagram.
- Identifying Outliers: Extreme Z-scores may indicate outliers. For example, the eighth video has Z-scores of -1.747361 and -1.38873, which are the lowest scores for both platforms, indicating that this video may be an outlier in terms of poor performance.
Conclusion : Data Transformation and Scaling
Z-Standardization has allowed us to compare the performance of the same videos across two different platforms with different rating scales. It provides insights into which videos performed well or poorly on both platforms and helps identify relative performance and potential outliers.
Step 3: Range Standardization To perform Range Standardization, you can use the following commands:
egen TikTok_Min = min(TikTok_Rating) egen TikTok_Max = max(TikTok_Rating) gen TikTok_Range = (TikTok_Rating - TikTok_Min) / (TikTok_Max - TikTok_Min) egen Instagram_Min = min(Instagram_Rating) egen Instagram_Max = max(Instagram_Rating) gen Instagram_Range = (Instagram_Rating - Instagram_Min) / (Instagram_Max - Instagram_Min)
This will create new variables with the range-standardized scores for both TikTok and Instagram ratings. You can use these scores for specific analyses like cluster analysis. When you check the data tab you will find the two columns with Standardized ratings for TikTok and Instagram like this
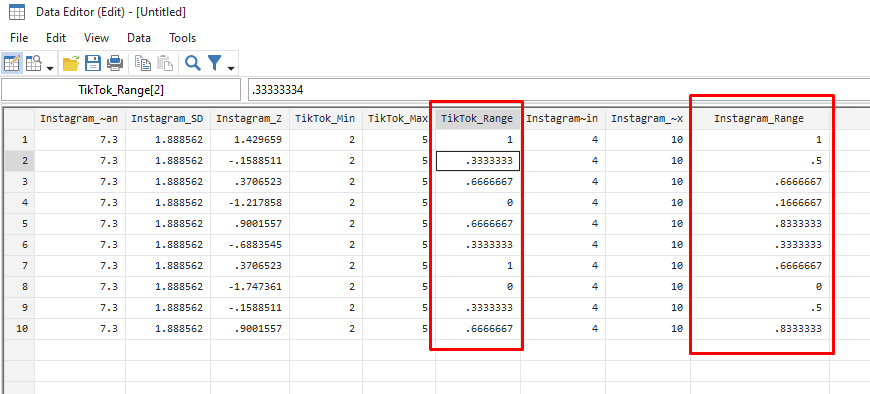
| Video_Number | TikTok_Range | Instagram_Range |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 0.3333333 | 0.5 |
| 3 | 0.6666667 | 0.6666667 |
| 4 | 0 | 0.1666667 |
| 5 | 0.6666667 | 0.8333333 |
| 6 | 0.3333333 | 0.3333333 |
| 7 | 1 | 0.6666667 |
| 8 | 0 | 0 |
| 9 | 0.3333333 | 0.5 |
| 10 | 0.6666667 | 0.8333333 |
Interpretation:
- Maximum and Minimum Values: The range standardization scales the data between 0 and 1. In this context, a score of 1 represents the best-performing video on a platform, and a score of 0 represents the worst-performing video.
- Comparing Performance Across Platforms: You can compare the Range-Standardized scores to see how a video performed relative to others on the same platform. For example, the first video received the highest score on both platforms, indicating top performance.
- Identifying Strengths and Weaknesses: By comparing the scores for each video across platforms, you can identify where the content is resonating more. For example, the second video has a higher Range-Standardized score on Instagram (.5) compared to TikTok (.3333333), indicating better relative performance on Instagram.
- Understanding Audience Engagement: The Range-Standardized scores can help you understand how different content engages audiences on different platforms. For example, the fourth video has the lowest score on both platforms, indicating that it may need to be re-evaluated or adjusted to better engage audiences.
Conclusion
Range Standardization provides a clear and comparable view of how videos performed across different social media platforms. It helps in identifying the best and worst-performing content and offers insights into where content may be resonating more with audiences.
5. Z-Standardization vs. Range Standardization
Let us now compare both the results we got in above analysis. I will make a critical comparison of both. Scaling in Stata
1. Methodology:
- Z-Standardization: Transforms the data to have a mean of 0 and a standard deviation of 1. It’s based on the mean and standard deviation of the data.
- Range Standardization: Scales the data between a specific range, usually 0 to 1. It’s based on the minimum and maximum values of the data.
2. Interpretation:
- Z-Standardization: The Z-scores provide insights into how many standard deviations a value is from the mean. Positive values indicate above-average performance, and negative values indicate below-average performance.
- Range Standardization: The Range-Standardized scores directly show the relative position of a value within the range of the data. A score of 1 represents the best performance, and a score of 0 represents the worst.
3. Sensitivity to Outliers:
- Z-Standardization: More sensitive to outliers, as extreme values can significantly affect the mean and standard deviation.
- Range Standardization: Less sensitive to outliers, as it only considers the minimum and maximum values.
4. Applications:
- Z-Standardization: Useful when you want to understand how data points relate to the overall distribution of the data. In our example, it helped compare video performance relative to the average.
- Range Standardization: Useful when you want to scale data within a specific range. In our example, it provided a clear comparison of video performance from worst to best.
6. Advantages & Disadvantages:
- Z-Standardization:
- Advantage: Consistency across different scales, allowing for comparison across platforms.
- Disadvantage: Potential loss of original scale information and sensitivity to outliers.
- Range Standardization:
- Advantage: Specific range scaling, useful for understanding relative performance.
- Disadvantage: Sensitivity to the choice of range, and extreme values can skew the transformation.
6. Conclusion:
- Z-Standardization is more suitable when you want to understand how each video performed relative to the overall distribution of ratings.
- Range Standardization is more suitable when you want a straightforward comparison of videos from worst to best.
Final Thoughts
Both Z-Standardization and Range Standardization have unique applications and can provide valuable insights depending on the context and the specific questions you are trying to answer. In the context of data analytics, understanding both methods allows for a more nuanced and comprehensive analysis of content performance across different platforms.
5. Common Mistakes in scale transformation and How to Avoid Them
Scale transformation might seem like a breeze, but watch out for these common pitfalls!
- Ignoring Outliers: Outliers can skew your transformation, especially in Range Standardization. Tip: Always check for outliers and consider how they might impact your analysis.
- Mixing Different Scales Without Transformation: Comparing apples to oranges? Not on our watch! Tip: Always use Z-Standardization or Range Standardization to make sure you’re comparing like with like.
- Overcomplicating the Process: Scale transformation doesn’t have to be rocket science. Tip: Stick to the basics and use tools like Stata to make the process smooth and straightforward.
Remember, a little caution goes a long way in making your scale transformation a success!
So for your reference I have made a diagram to summarize everything that we learnt.
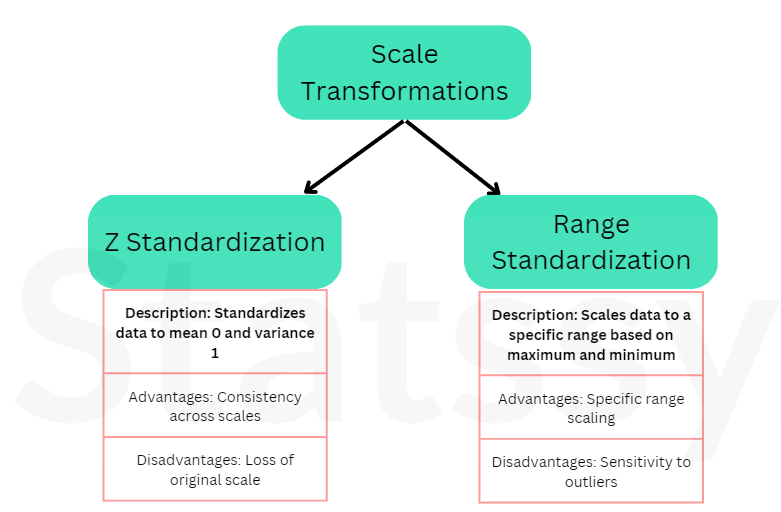
6. Conclusion
And there you have it! Scale transformation is more than just a fancy term; it’s the key to unlocking meaningful insights from your social media data.
From understanding viral TikTok dances to analyzing Instagram food trends, scale transformation helps you see the big picture. It’s like having a translator for different rating scales, making sure you’re always in the know.
So, what are you waiting for? Dive into your data, explore those trends, and don’t be shy to share your experiences or ask questions in the comments below. We’re all in this together, learning and growing in the ever-evolving world of data analytics!
If you found this guide on scale transformation in Stata helpful, you may also be interested in our other Stata tutorials. Learn the basics with our Beginner’s Guide to Mastering Descriptive Statistics in Stata. If you’re looking to dive deeper into customer analytics, don’t miss our article on Leveraging Coefficient of Variation in Customer Analytics: A Stata Example. And for a straightforward business application, check out Calculating the Coefficient of Variation in Stata: A Simple Business Example.
